球内・球面上のパターン形成

論文：投稿中

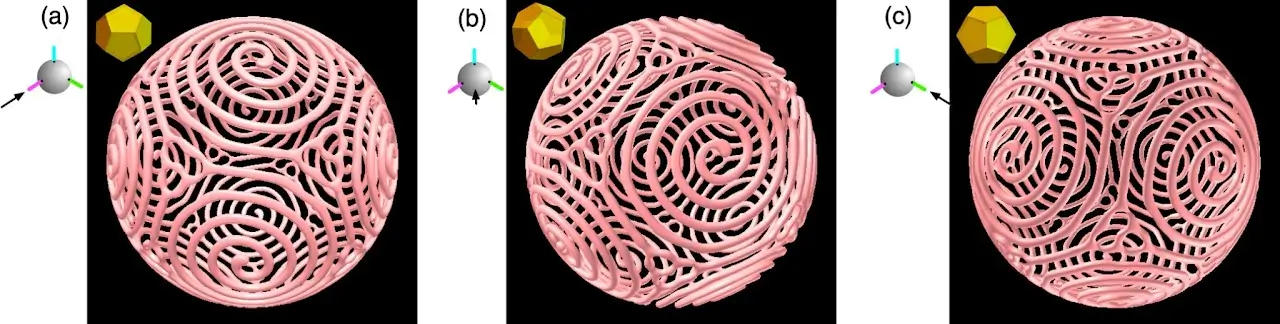
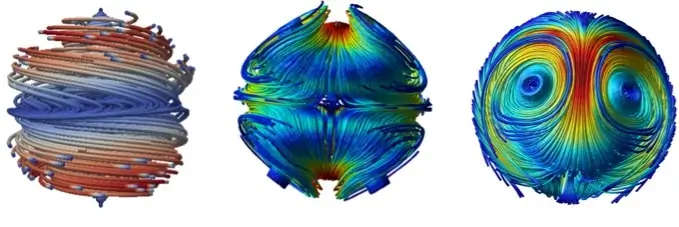
薄い球殻内部の熱対流の新しい安定定常解を見つけました。これは正12面体の表面に6対のアルキメデス螺旋が乗ったパターンです。カイラルな（鏡像変換に対して対象でない）であることが特徴です。下の図は定常状態の対流パターンを3つの異なる方向から見たものです。対流の上昇流の等値面をVISMO-YYというin situ可視化ライブラリで可視化しています。

4次元ストリートビュー

論文：PeerJ Computer Science (2020); Computer Physics Communications (2014)

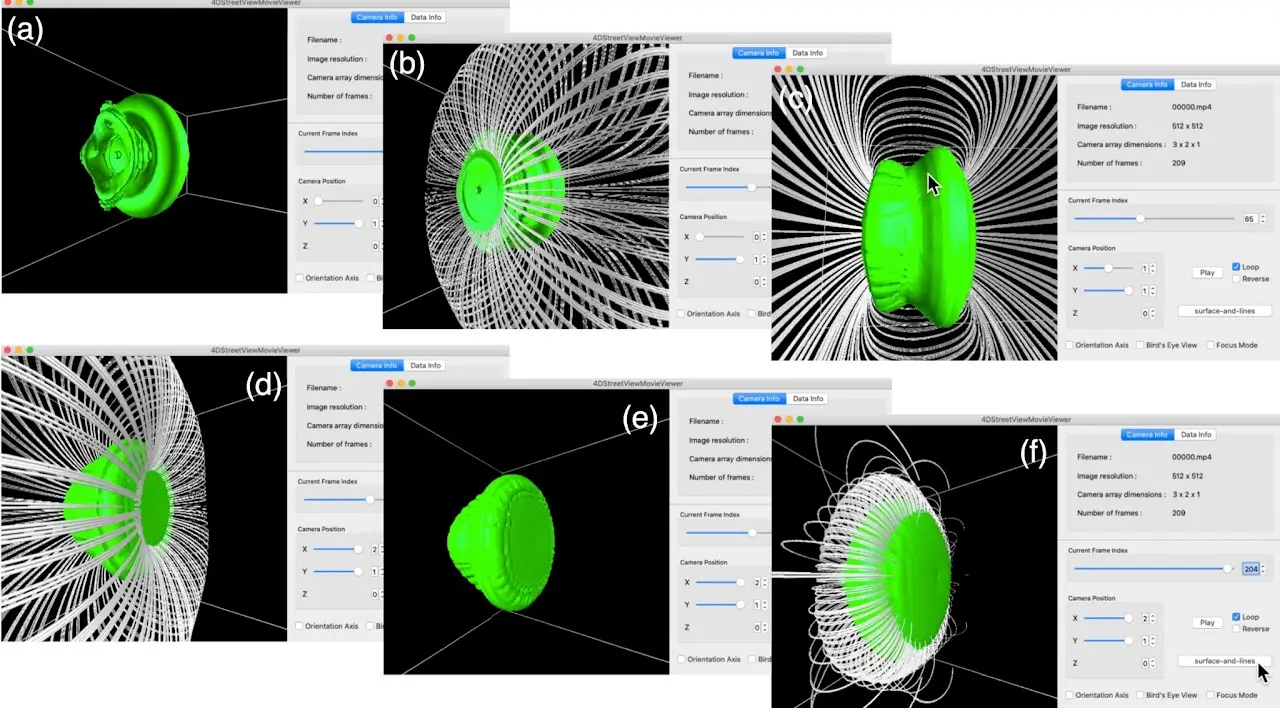
大規模な計算機シミュレーションは今後in situ可視化が主流となるでしょう。in situ可視化に対話性を導入するために「4次元ストリートビュー」という新しい可視化のスタイルを提案しました。

表面張力進行波によるねじれた水流の形成

論文：Phys. Rev. Fluids (2020)

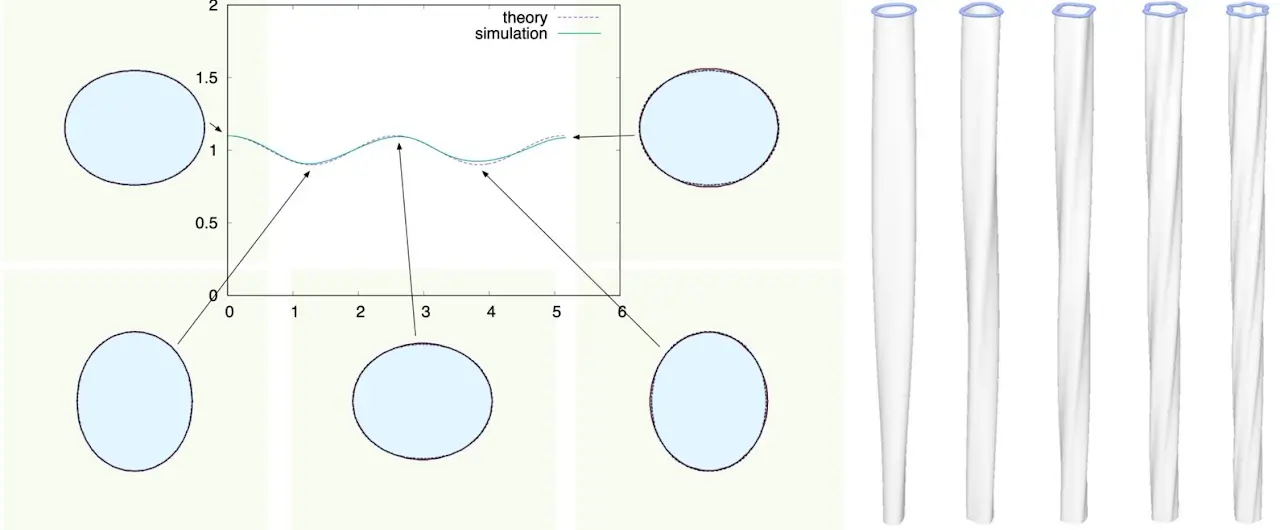
これは当時高校生だった後藤優奈さんとの共同研究です。蛇口から流れ落ちる円柱状の水流が表面張力によって振動する現象は日常よく目にします。この論文では、蛇口の形状を少し工夫することで、円柱の周方向に進行する表面張力波を誘起することができることを示しました。これによりねじれた形状の水流ができます。この研究ではProcessingを使って計算しました。

磁気流体の自己組織化

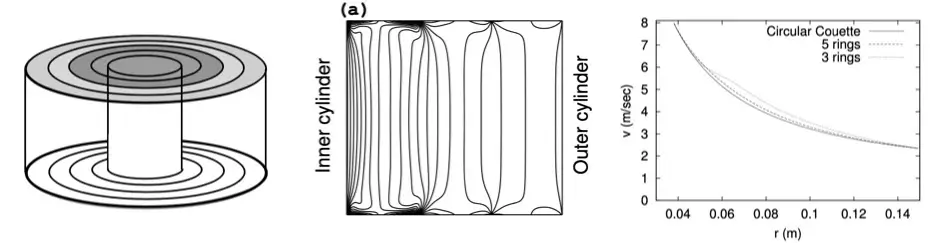
球内部のMHD流体の緩和状態を調べました。流れと磁場が等エネルギー状態で共存する興味深い構造を見出しました。

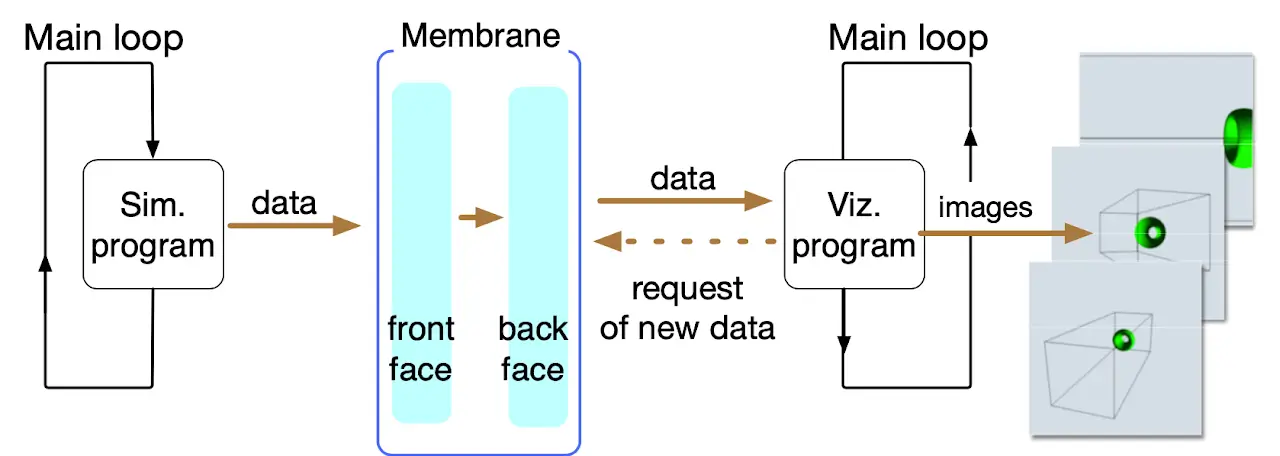
非同期in-situ可視化のための半透膜手法の開発

論文：Lecture Notes in Computer Science (2019)

スーパーコンピュータ上で非同期にin-situ可視化を実現するための半透膜アナロジーに基づくインターフェース手法を開発しました。

Fortran2003の「方言」 eFortran とプリプロセッサefppの開発

論文：Communications in Computer and Information Science (AsiaSim, 2018)

モダンFortranを書きやすくするためのプリプロセッサを作りました。

4次元物体の3次元「断面」による可視化

論文：Journal of Visualization (2016)

4次元データの3次元可視化をめざしたものです。

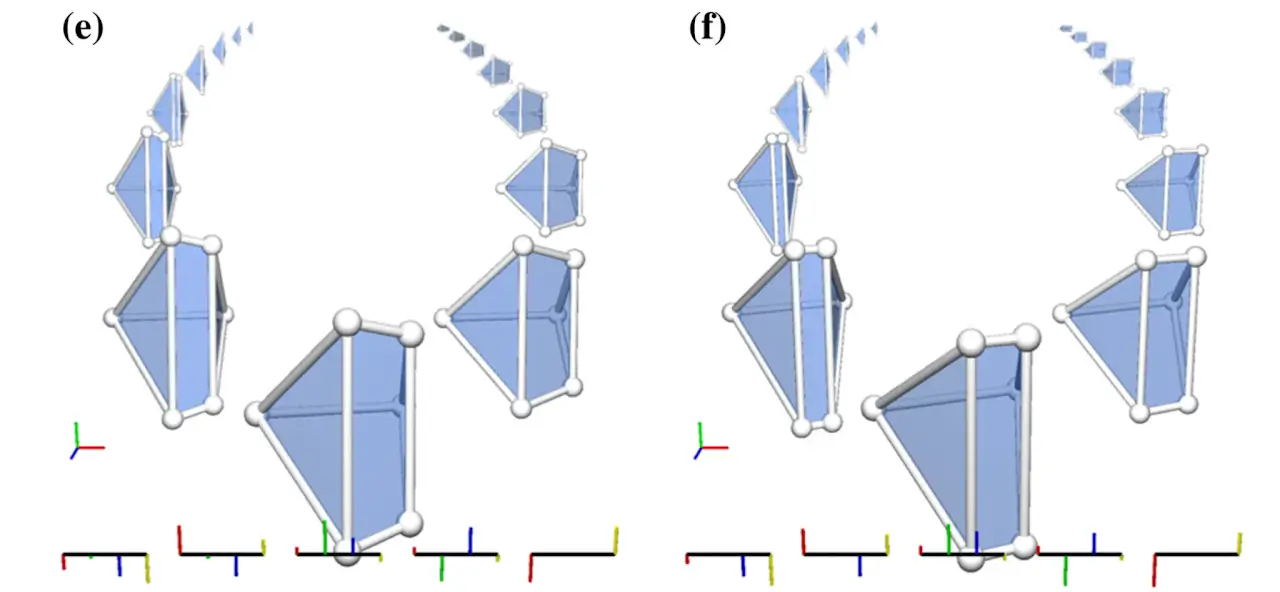
Yin-Yang-Zhong格子の考案

論文：J. Comput. Phys. (2016)

以前考案したYin-Yang格子を改良し、球全体を解けるようにしました。

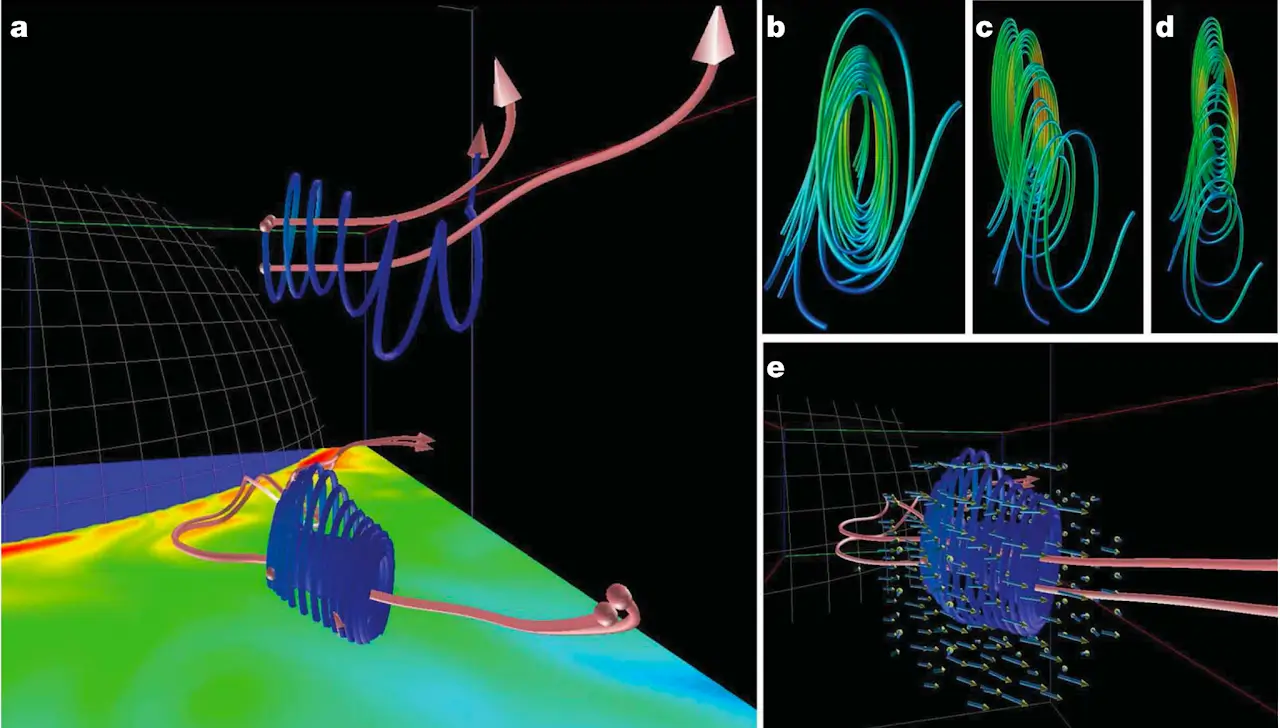
地磁気シミュレーション関係

論文：Nature (2010, 2008); Science (2002); Phys. Rev. Lett. (1999); Phys. Rev. E (1997); Phys. Plasmas (1995)

CAVE型VR装置を使った3次元可視化

論文：IJMSS (2016, 2013); Prog. Theor. Phys. Supplement (2000)

修正ダイポール座標の考案

論文：Computers & Geosciences (2006)

コリオリ力（あるいは回転系のMHD方程式に見かけの磁場誘導項がないこと）のオイラー的導出

論文：G-cubed (2006)

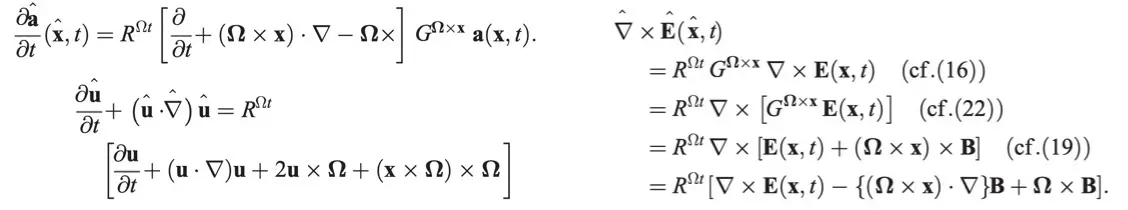
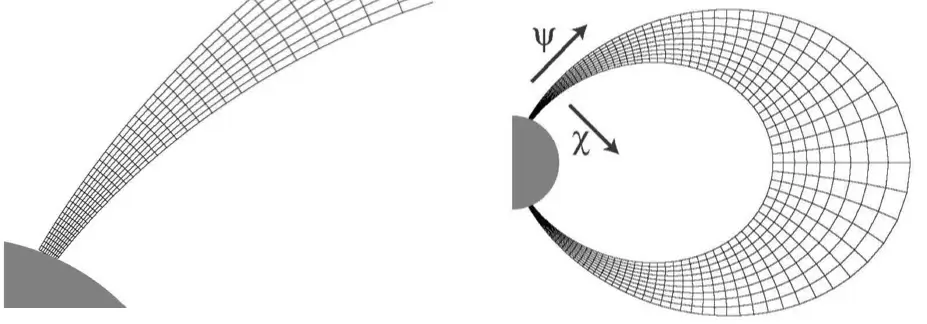
インヤン（Yin-Yang）格子の考案

論文：G-cubed (2004)

回転流体のエクマン循環とその抑制法

論文：J. Phys. Soc. Japan (2004)